Eliminating Isomorphic Solutions from Knight's Tour of Chessboard
Introduction :
When Knight’s tour solutions are generated on a mass scale (using some algorithm/s) it is well understood that all the solutions so obtained are not going to be non-isomorphic, even within any single given set. Two methods have been developed (and perfected) for comparing any solutions to detect isomorphism. Only one method has been described in this paper. Using it, work has been done to isolate non-isomorphic solutions called out as Independent Solutions or Original Solutions. Work is going on to extend the collection.
Previous Work Done :
The problem of Knight’s Tour of the chessboard, being at least 5 centuries (perhaps 11 centuries also) old, has been widely worked on. A simple search using the Google® Search Engine easily detects several thousand significant results (web-pages). I have visited several hundred such web-pages. I have not found any work similar to the one presented here.
I have published a book[1] in which a full chapter is devoted to this subject. All the material in this paper has been extracted from the book.
Background :
An exhaustive analysis of Warnsdorff’s rule was carried out by me, for closed solutions. A computer program was specifically developed for the same. The details are available in another paper on this website. While working, it was realized that in the solutions generated using Warnsdorff’s rule, there could be a large number of isomorphic solutions. To detect and eliminate isomorphic solutions, two methods were developed. One of them is presented here
Isomorphism in Knight’s Tours :
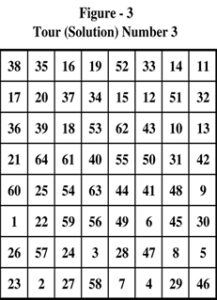
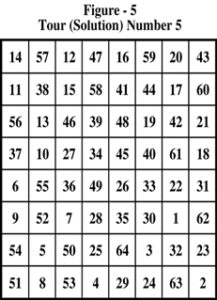
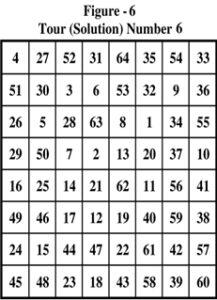
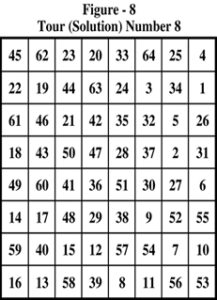
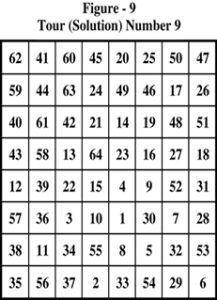
Study the 9 closed tours presented in Figure – 1 through Figure – 9. Are the solutions presented isomorphic or non-isomorphic?
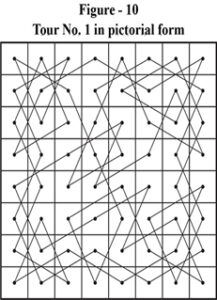
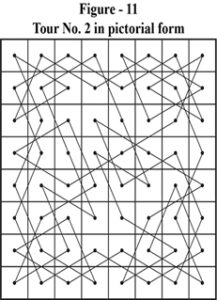
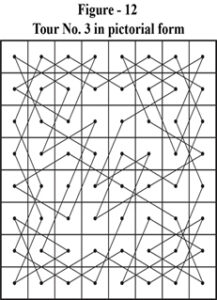
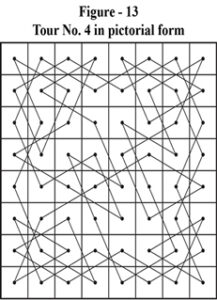
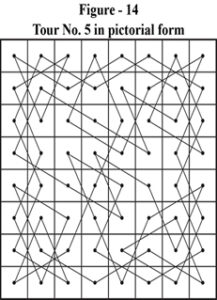
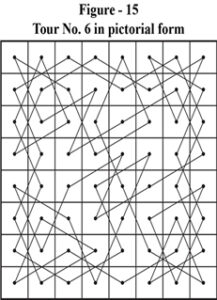
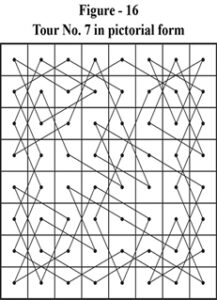
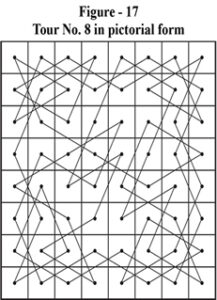
To answer this simple question a lot of work is necessary. We need to represent the solutions in pictorial form. The solutions of figure – 1 through figure – 9 are pictorially represented as Figure – 10 through Figure – 18.
Advantage of pictorial representation is that there is no starting or ending point. The entire tour in closed form appears in the picture. If we are able to compare the pictures with one another, we can easily detect occurrence of a solution that has appeared before. Manual way of doing this is to plot each solution on a transparent paper so that the comparison can be done easily and conveniently by rotating or flipping over the paper. Manually, the task of just plotting 54,234,604 pictures would be a stupendous one let alone the subsequent comparison! However, at the moment, we have only 9 solutions to compare. Let us do it manually.
Immediately, we find that the 9th solution of figure 9 (or figure – 18) is identical with the 1st solution of figure – 1 (or figure – 10). The numbering of cells is done differently. Also, the travel of the knight is in opposite direction to that of figure – 1. It is difficult, if not impossible, to detect the isomorphism without pictorial representation of both solutions.
Continuing further, we find that
- Clockwise Rotation of figure 10 through 90° gives us figure – 11.
- Anticlockwise Rotation of figure 10 through 90° gives us figure – 13.
- Rotation of figure 10 through 180° gives us figure – 15.
- Mirror Image of figure 10 in a Vertical Mirror placed parallel to Right or Left side of the board gives us figure – 16.
- Mirror Image of figure 10 in a Horizontal Mirror placed parallel to Top or Bottom side of the board gives us figure – 14.
- Mirror Image of figure 10 in a mirror placed parallel to Top-Left to Bottom-Right (TL-BR) Principal Diagonal gives us figure – 12.
- Mirror Image of figure 10 in a mirror placed parallel to Top-Right to Bottom-Left (TR-BL) Principal Diagonal gives us figure – 17.
Any solution of the full tour can thus exist in any one of the 9 forms. Hence, the solution that occurs first (figure 1) in the set is called the independent or original solution. All other solutions occurring later and being the same as earlier one or obtained by transformation (in one of the 8 ways as above) of the original are isomorphic with the original. The latter, also called duplicate solutions, should be eliminated from the set as being isomorphic or non-independent.
An algorithm has been developed and a computer program was written to do the menial job of plotting and comparing the solutions. Even then, as the original solutions start getting accumulated, the running time for the program goes on increasing. Suppose a few solutions have been identified as independent and are stored in a file. A new solution (a candidate) is to be compared to decide whether it is independent or a duplicate. It becomes necessary to compare the candidate itself and all the seven other variations of this candidate with all the earlier recorded original solutions. If the independent solutions file contains 100 solutions, 8 variations of the candidate solution are to be compared with all the 100 originals. There are thus 800 sets compared. Each set has 64 moves to be compared. As the original solutions become 1,000, the number of comparisons becomes 8,000.
Elimination of Duplicate (Isomorphic) Solutions :
For manual comparison, we saw how plotting the solutions on transparent paper was necessary. For computer comparison, each solution needs to be represented in a numerical form. Only then, the two sets of numbers can be compared in a computer program.
Two methods were devised for representing any solution on computer. First method is termed as the “Co-ordinate Method” and the second one is termed as “Move Number Method”. Both methods have been successfully used for the first 40,000+ original solutions. When the number of independent solutions found from first 16 sets was the same by both methods, the second method was discontinued. Thereafter, only first method was used with some more improvements.
Co-ordinate Method of Representation :
Pictorial representation of first solution was given earlier in figure 10. In this, each move is represented as a line joining the centers of the two cells. Once the closed tour is completed, it is immaterial whether the knight went from cell a to cell b or vice versa. In the pictorial form, what we see is that each cell is connected with exactly two other cells, by knight’s moves. Rather than noting the move/s, the connectivity is mathematically represented as a number. This number is made up from the co-ordinates of the two connected cells.
The co-ordinate system followed is such that the rows are numbered from top to bottom and the columns are numbered from left to right. Thus, the topmost row leftmost cell has co-ordinates (1,1) and bottom-most row rightmost cell has co-ordinates (8,8). Naturally, all co-ordinates lie between these limits. For brevity, the cell (1,1) is simply written as 11 and cell (8,8) becomes 88. All the cell numbers fall between these two limits.
A move between cells 11 and 23 is represented as single four-digit number 1123 whether the move is from 11 to 23 or whether it is from 23 to 11. This is because we are recording the connectivity and not the actual move/s. This way, even if the two tours are in directions opposite of each other, both the tours will be represented by same set of numbers.
Numerically lower co-ordinate is always taken first. The tour is thus transformed into a set of 64 four-digit numbers. These numbers are then sorted in ascending order and then stored. When two tours are compared, the 64 numbers of one tour are compared with the 64 numbers of the other tour. The tours are same only if all the 64 numbers are identical, otherwise the tours are different. Since all the 64 numbers are to be identical, even if a single mismatch is found during comparison, further comparison can be safely abandoned and the tours can be declared different.
When the first solution of figure – 1 (pictorial representation of figure – 10) is transformed into 64 connectivity numbers using end co-ordinates, the generated numbers are shown in Figure – 19.

When seven other variations (mirror images & rotations) are to be created from a solution (so that all the variations of a candidate can be compared with a known original solution), suitable transformations of the 64 numbers are carried out and the new set of 64 is created. This new set is used for comparison. Let us also see how the numerical transformations are done.
Let “I” represent the new row co-ordinate of any cell after transformation which had i as the row co-ordinate before transformation and let J represent the new column co-ordinate of any cell after transformation which had j as the column co-ordinate before transformation. Then the relationships for different transformations can be summarized as follows :
| Transformation | Relationships | |
|---|---|---|
| Image in vertical mirror | I = i | J = 9 – j |
| Image in horizontal mirror | I = 9 – i | J = j |
| Image in TL-BR diagonal mirror | I = j | J = i |
| Image in TR-BL diagonal mirror | I = 9 – j | J = 9 – i |
| Clockwise rotation through 90° | I = j | J = 9 – i |
| Anticlockwise rotation through 90° | I = 9 – j | J = i |
| Rotation through 180° | I = 9 – i | J = 9 – j |
On further thinking in 2005, it was realized that 8 connections around the four corners will be common to each closed solution. The moves are 1123, 1132, 1826, 1837, 6281, 6788, 7381 and 7688. If we remove these connections from the 64, only 56 numbers need to be compared instead of 64. This facilitated cutting down on comparison time.
Storage and Handling of Solution Files :
If the solutions are stored in the form of figures – 1 through 9, too much of disk space would be required just to store the solutions. A different method was hence devised for the storage on mass scale. Each solution occupies one line in a file. Two spaces followed by sixty four row co-ordinates are first written, each number being a single digit less than or equal to 8. This is followed by two spaces. Then, sixty four column co-ordinates are written. The solution file is in ASCII format. Along with the “carriage-return-line-feed” character, each line (one solution) takes 134 bytes. This file is termed as a “compact file” for solutions.
Suppose we have a candidate solution which is to be compared with already stored independent solutions for knowing whether the candidate is an independent solution or a duplicate one. Let us assume that this solution is placed in a compact file.
A program has been developed to convert this compact file into 8 different “expanded” files. Each file, after a space, holds 56 four-digit connectivity numbers in one line, generated by end co-ordinate method of conversion described above. Needless to say, these 56 numbers are sorted in an ascending order before storing. Each line takes 227 bytes inclusive of carriage-return-line-feed character at the end of the line. These files are also in ASCII format.
The first expanded file contains the candidate solution itself converted into connectivity numbers. The second file contains similar 56 numbers obtained by clockwise rotating the candidate solution through 90°. The third file has 56 numbers obtained by taking a mirror image of the candidate solution by placing the mirror along (or parallel) to the principal diagonal TL-BR. Similarly, the remaining files hold 56 numbers obtained by other transformations of the candidate solution.
Now suppose we have already isolated 4,000 independent solutions and the candidate is to be compared with these master solutions. These “master” solutions are placed in a master file with 4,000 lines. Each master solution occupies one line and contains 56 four-digit numbers obtained by converting the master solution by co-ordinate method. At the time of comparison, entire master file is read and stored in a matrix. The candidate solution is read and is compared with the first master solution. If they are different, candidate’s next transformation is compared with the first master solution. This way, all 8 variations of the candidate are compared with the first master solution. When there is no match, the candidate is compared with the second master solution and so on.
When there is a match between a candidate (or its transformation) with a master, serial number of the candidate (in candidate’s file), serial number of master solution (in master’s file) and the variation number (1 to 8) of the candidate are all stored in a special file. This way, at the end of the comparison run, all the duplicate solutions are reported. The duplicate solutions are then eliminated from the candidates file with the help of another computer program.
Results of Comparison :
The comparison work done by me is restricted to closed tours obtained by use of Warnsdorff’s rule and some variations of the rule. It is observed that using the rule, the knight tends to remain within outer two rows, at least during the first half of the tour. This creates lot of duplicate solutions. Therefore, proportion of independent solutions is quite small. Incidentally, covering the outer two rows first is also a method suggested by De Moivre[2]. It is my guess that if solutions are generated using De Moivres method, there would be a large proportion of duplicate solutions in that set also.
With 10 independent starting points and corresponding 53 ending points (to make the tour closed), I have generated 54,234,604 total solutions by Warnsdorff’s rule and some variations of the rule. The details of this work are given in another paper on this website. Additional details can be found in tables with names AlgoMain, AlgoECD and AlgoXCD by following an appropriate link.
The present (final) tally of independent solutions stands at 3,671,161 as on 22nd February 2024. In this, in all, 54,234,604 solutions from 22,432 sets have been covered. Only 6.77% of the solutions compared are original (independent, non-isomorphic). The work is now completed.
The master solutions are placed in 368 files. The first 367 files store 10,000 solutions each. The last master file has only 1,161 solutions. The summary of the comparison work done is given in Table – 1. All the non-isomorphic solutions have been rechecked to ensure that not a single isomorphic solution has infiltrated into the collection!
Comparison of Open Tour Solutions :
The work presented above is strictly for closed tours only. The beauty of co-ordinate system is such that it can be used for comparison of open tour solutions too.
In a closed tour, there are 56 connections (from 64 moves) to be compared between two solutions. This makes the comparison relatively simpler. In an open tour, there are only 63 moves made by the knight. This makes the comparison (only) slightly more difficult. It is proposed that a fictitious (pseudo) move be made. Let the fictitious move, rather its connectivity, be represented by a line joining the starting cell with the ending cell, wherever the latter may be. Thus, once again, we have 64 moves for each solution and 64 connections including the fictitious one.
As before, the co-ordinate method of representation can be used for storing the solution and the same method of comparison can be followed. Again, the compared solutions are isomorphic only if all the 64 “moves” (including the fictitious one) are identical.
There is a major difference here. In the work presented, only 56 moves could be compared for detection of isomorphism. For open tours, no such shortening of work is possible. The tour could very well start or end at one or more corner/s and/or on the corner approach cell/s. Therefore, all the 64 moves must be compared.
The second method devised by this author, “Move Number Method”, cannot be used for comparison of open tours. Therefore, this paper deals with only the co-ordinate method.
An example will make the concepts clear. Consider an open tour (solution) as in Figure – 20. This example is taken from a book by Rouse Ball[2]. The starting and ending points are 5 rows apart. The tour in pictorial form is shown in Figure – 21. A line (not by knights move) joins the starting point (1) with the ending point (64). The connectivity of this figure is created by using co-ordinate method, to get Figure – 22. We now have a set of 64 connectivity numbers to represent this solution. In a similar manner, connectivity numbers can be generated for any open tour solution.
Comparison of connectivity numbers of two tours can tell us whether they are isomorphic or not.
References :
[1] Phadke, Pramod S., Computer Programs for Solving Mathematical Puzzles, Self-Published, 2007. Chapter – 11, p 86 – 114.
[2] Rouse Ball, W.W., Mathematical Recreations and Essays, 11th Edition, Reprinted 1940, p 174 – 185.